Cách viết phương trình đường tròn nội tiếp tam giác – Toán 10 chuyên đề

Cùng cmm.edu.vn tìm hiểu Cách viết phương trình đường tròn nội tiếp tam giác – Toán 10 chuyên đề

Vậy cách viết phương trình đường tròn nội tiếp tam giác như thế nào? làm sao để viết phương trình đường tròn một cách chính xác và không bị nhầm lẫn?Nếu chưa nắm vững kiến thức lý thuyết, các em có thể tham khảo bài viết này: Kiến thức về phương trình đường tròn và các dạng toán

Bạn đang xem bài: Cách viết phương trình đường tròn nội tiếp tam giác – Toán 10 chuyên đề

Còn ngay bầy giờ, chúng ta cùng tìm hiểu cách viết phương trình đường tròn nội tiếp tam giác.

* Phương pháp:

° Cách 1:

– Tính diện tích S và nửa chu vi P của tam giác để tính được bán kính đường tròn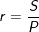

– Gọi I(a;b) là tâm của đường tròn nội tiếp thì khoảng cách từ I tới 3 cạnh của tam giác bằng nhau và bằng r, từ đó lập thành hệ pt với 2 ẩn a, b.

– Giải hệ phương trình ta tìm được giá trị của a, b và phương trình đường tròn.

° Cách 2:

– Viết phương trình đường phân giác trong của 2 góc trong tam giác.

– Tìm giao điểm 2 đường phân giác đó ta được tâm I của đường tròn

– Tính khoảng cách từ I tới 1 cạnh bất kỳ của tam giác ta được bán kính.

* Ví dụ 1:Cho 2 điểm A(4;0) và B(0;3)

a) Viết phương trình đường tròn ngoại tiếp tam giác OAB

b) Viết phương trình đường trònnộitiếp tam giác OAB

* Lời giải:

a) Tam giác OAB vuông tại O nên tâm của đường tròn ngoại tiếp tam giác tam giác OAB là trung điểm của cạnh huyền AB nên tâm toạ độ tâm I của đường tròn nội tiếp là: I=(2;3/2).

⇒ Bán kính: R = IA = 5/2

⇒ PT đường tròn ngoại tiếp tam giác OAB là: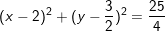

b) Ta sẽ tính diện tích và nửa chu vi của OAB

– Ta có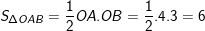

– Nửa chu vi: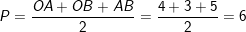

⇒

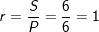
– Vì đường tròn tiếp xúc với 2 trục toạ độ nên tâm Ir=(r;r)=(1;1)

⇒ Pt đường tròn là: (x – 1)²+ (y – 1)²= 1

* Ví dụ 2:Viết phương trình đường tròn nội tiếp tam giác ABC tạo bởi 3 đường thẳng:

(d1): 4x – 3y – 65 = 0

(d2): 7x – 24y + 55 = 0

(d3): 3x + 4y – 5 = 0

* Lời giải:

– Gọi ABC là tam giác đã cho với các cạnh là:

AB: 4x – 3y – 65 = 0

BC: 7x – 24y + 55 = 0

CA: 3x + 4y – 5 = 0

– Ta tính được A(11;-7), B(23;9), C(-1;2)

– Ta có VTPT:,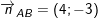

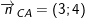
– Dễ thấy tam giác vuông tại A do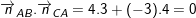

– Tính độ dài các cạnh ta có: AB = 20 ; BC = 25; CA = 15

– Diện tích tam giác ABC: SABC= 150

– Nửa chu vi là: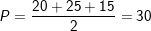

– Bán kính đường tròn nội tiếp là: r = S/P = 150/30 = 5.

– Gọi bán kính đường tròn nội tiếp là I(a;b) thì khoảng cách từ I tới các đường thẳng đã cho đều là r=5 nên ta có.

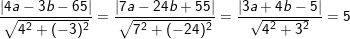
– Giải hệ trên ta được: a = 10 và b = 0;

⇒ Phương trình đường tròn cần tìm là: (x – 10)²+ y²= 25

>> xem thêm: Các dạng toán về phương trình đường tròn

Như vậy với cách viết phương trình đường tròn nội tiếp tam giác ở trên, cùng các ví dụ cụ thểcmm.edu.vn hy vọng bài viết giúp ích cho các em. Mọi góp ý và thắc mắc các em vui lòng để lại bình luận dưới bài viết để cmm.edu.vn.Vn ghi nhận và hỗ trợ, chúc các em học tập tốt.

Trích nguồn: Cao đẳng Tài nguyên và Môi trường miền Trung
Danh mục: Giáo dục