Cùng cmm.edu.vn tìm hiểu Cách tìm hình chiếu của 1 điểm lên đường thẳng trong Oxy – Toán 10 chuyên đề
Vậycách tìm hình chiếu của 1 điểm lên đường thẳng trong Oxy như thế nào?chúng ta sẽ cùng tìm hiểu qua bài viết dưới đây và cùng xem các bài tập và ví dụ minh họa để hiểu rõ nhé.
Bạn đang xem bài: Cách tìm hình chiếu của 1 điểm lên đường thẳng trong Oxy – Toán 10 chuyên đề
Các em có thể xem lại nội dungphương trình tổng quát, phương trình tham số, phương trình chính tắc của đường thẳngnếu các em chưa nhớ rõphần kiến thức này.
° Cách tìm hình chiếu của 1 điểm lên đường thẳng trong Oxy
* Cách giải 1:
•Giải sử cần tìm hình chiếu H của điểm M lên đường thẳng (d), ta làm như sau:
– Lập phương trình đường thẳng (d’) qua M vuông góc với (d). (các em có thể xem lạicách viết phương trình đường thẳng đi qua 1 điểm vuông góc với 1 đường thẳng).
– H là hình chiếu vuông góc của M lên (d)⇒ H là giao của (d) và (d’).
* Cách giải 2:
•Giải sử cần tìm hình chiếu H của điểm A lên đường thẳng (d): ax + by + c = 0ta làm như sau:
+ Bước 1: Gọi tọa độ điểm H(xH; yH).
Vì điểm H thuộc (d) nên: axH+ byH+ c = 0 (1).
+ Bước 2: Do AH vuông góc d nên
là VTPT của (d), tức là:
=(xH– xA; yH– yA) và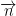
=(a; b) cùng phương
⇒ b(xH– xA) – a(yH– yA)= 0 (2)
+ Bước 3: giải hệ(1) và (2) ta được tọa độ điểm H.
* Ví dụ 1:Tìm hình chiếu của điểm M(3;-1) lên đường thẳng (d) có phương trình: x + 2y – 6 = 0
* Lời giải:
¤ Giải theo cách 1:
– Gọi (d’) là đường thẳng đi qua M và vuông góc với (d)
– Vì (d) có phương trình: x + 2y – 6 = 0 nên VTPT của (d) là: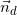
= (1;2)
– Lại có (d’)⊥ (d) nên (d’) nhận VTPT của (d) là VTCP⇒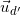
=(1;2)
– Phương trình đường thẳng (d’) qua M(3;-1) có VTCP 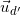(1;2) là:
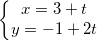
– Vì H là hình chiếu của M thì H là giao điểm của (d) và (d’) nên có:
Thay x,y từ (d’) và phương trình (d), ta có:
(3+t) + 2(-1+2t) – 6 = 0
⇔ 5t – 5 = 0⇔ t =1
⇒ x = 4, y = 1 là toạ độ điểm H.
Vậy tọa độ H(4;1)
* Ví dụ 2:Tìm hình chiếu của điểm M(1;3) lên đường thẳng (d): x – y = 0
* Lời giải:
¤ Giải theo cách 1:
– Gọi (d’) là đường thẳng đi qua M và vuông góc với (d)
– Vì (d) có phương trình: x – y = 0 nên VTPT của (d) là: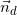= (1;-1)
– Lại có (d’)⊥ (d) nên (d’) nhận VTPT của (d) là VTCP⇒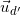=(1;-1)
– Phương trình đường thẳng (d’) qua M(1;3) có VTCP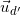(1;-1) là:
– Vì H là hình chiếu của M thì H là giao điểm của (d) và (d’) nên có:
Thay x,y từ (d’) và phương trình (d), ta có:
(1 + t) – (3 – t) = 0
⇔ 2t = 2⇔ t = 1
Vậy tọa độ H là: (2;2)
¤ Giải theo cách 2:
+ Gọi H(a;b) là hình chiếu của M lên (d).
+ Do H ∈ (d) nên ta có: a – b = 0 (1)
Ta có:
= (a – 1; b – 3)
Đường thẳng MH vuông góc với (d) nên:
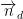= (1;-1) cùng phương với= (a – 1; b – 3)
hay VTCP: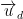
=(1;1)⊥= (a – 1; b – 3)
Suy ra: 1.(a – 1) + 1.(b – 3) = 0
⇔ a + b = 4 (2)
Từ (1) và (2) suy ra: a = 2; b = 2
Vậy tọa độ của H(2;2)
>> xem ngay:Các dạng bài tập phương trình đường thẳng trong mặp phẳng Oxy
Hy vọng với bài viếtCách tìm hình chiếu của 1 điểm lên đường thẳng trong Oxyở trên hữu ích cho các em. Mọi thắc mắc các em vui lòng để lại bình luận dưới bài viết để cmm.edu.vn.Vn ghi nhận và hỗ trợ. Chúc các em học tập tốt!
Trích nguồn: Cao đẳng Tài nguyên và Môi trường miền Trung
Danh mục: Giáo dục
