7 hằng đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình học toán, các bạn trẻ được tiếp xúc đầu tiên ngay từ khi bắt đầu lên lớp 8 và khi lên các lớp cao hơn thì bảy đẳng thức đáng nhớ được áp dụng trong các bài toán nâng cao nhiều hơn, và theo các bạn suốt quãng đường học tập. 7 hằng đẳng thức đáng nhớ giống như cái tên gọ của nó, “đáng nhớ” ở đây và thể hiện vai trò của nó trong việc tiếp thu kiến thức của các bạn trẻ, hằng đẳng thức là công cụ đem lại nhiều lợi ích khi áp dụng vào môn toán ở chương trình học tập.

Công thức về 7 hằng đẳng thức
1. Bình phương của một tổng
(A + B)2 = A2 + 2AB + B2
Giải thích: Bình phương của một tổng bằng bình phương của số thứ nhất cộng với hai lần tích của số thứ nhất nhân với số thứ hai, cộng với bình phương của số thứ hai
Bạn đang xem bài: 7 Hằng Đẳng Thức Đáng Nhớ và các dạng toán áp dụng
* Ví dụ Bài 16 trang 11 sgk toán 8 tập 1: Viết dưới dạng bình phương của 1 tổng hoặc 1 hiệu
a) x2 + 2x + 1 = (x)2 + 2.(x).(1) + (1)2 = (x+1)2
b) 9x2 + y2 + 6xy = 9x2 + 6xy + y2 = (3x)2 + 2.(3x).(y) + (y)2 = (3x+y)2
2. Bình phương của một hiệu
(A – B)2 = A2 – 2AB + B2
Giải thích: Bình phương của một hiệu bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất nhân số thứ hai sau đó cộng bình phương với số thứ hai.
* Ví dụ Bài 16 trang 11 sgk toán 8 tập 1: Viết dưới dạng bình phương của 1 tổng hoặc 1 hiệu
c) 25a2 + 4b2 – 20ab = 25a2 – 20ab + 4b2 = (5a)2 – 2.(5a).(2b) + (2b)2 = (5a+2b)2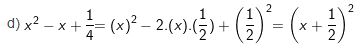
3. Hiệu hai bình phương
A2 – B2 = (A – B)(A + B)
Giải thích: Hiệu hai bình phương của hai số bằng tổng hai số đó nhân với hiệu hai số đó.
* Ví dụ: Viết dưới dạng tích biểu thức: 4x2 – 9
* Lời giải:
– Ta có: 4x2 – 9 = (2x)2 – (3)2 = (2x-3)(2x+3)
4. Lập phương của một tổng
(A + B)3 = A3 + 3A2B + 3AB2 + B3
Giải thích: Lập phương của một tổng hai số bằng lập phương của số thứ nhất cộng với ba lần tích bình phương số thứ nhất nhân số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai cộng với lập phương số thứ hai.
* Ví dụ Bài 26 trang 14 sgk toán 8 tập 1: Tính
a) (2x2+3y)3 =(2x2)3 + 3(2x2)2.(3y) + 3(2x2).(3y)2 + (3y)3 = 8x6 + 36x4y + 54x2y2 + 27y3
5. Lập phương của một hiệu
(A – B)3 = A3 – 3A2B + 3AB2 – B3
Giải thích: Lập phương của một hiệu hai số bằng lập phương của số thứ nhất trừ đi ba lần tích bình phương của số thứ nhất nhân với số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai trừ đi lập phương số thứ hai
* Ví dụ Bài 26 trang 14 sgk toán 8 tập 1: Tính
6. Tổng hai lập phương
A3 + B3 = (A + B)(A2 – AB + B2)
Giải thích: Tổng của hai lập phương hai số bằng tổng của hai số đó nhân với bình phương thiếu của hiệu hai số đó
* Ví dụ: Viết dưới dạng tích x3 + 64
x3 + 64 = x3 + 43 = (x+4)(x2-4x+42) = (x+4)(x2-4x+16)
7. Hiệu hai lập phương
A3 – B3 = (A – B)(A2 + AB + B2)
Giải thích: Hiệu của hai lập phương của hai số bằng hiệu hai số đó nhân với bình phương thiếu của tổng của hai số đó.
* Ví dụ: Viết dưới dạng tích 8x3 – y3
8x3 – y3 = (2x)3 – y3 = (2x-y)[(2x)2 – (2x).y + y2] = (2x-y)(4x2 + 2xy + y2)
* Chú ý: a+b= -(-a-b) ; (a+b)2= (-a-b)2 ; (a-b)2= (b-a)2 ; (a+b)3= -(-a-b)3 ; (a-b)3=-(-a+b)3
Các dạng bài toán áp dụng 7 hằng đẳng thức
Dạng 1 : Tính giá trị của biểu thức
Ví dụ: Tính giá trị của biểu thức : A = x2 – 4x + 4 tại x = -1
* Lời giải.
– Ta có : A = x2 – 4x + 4 = x2 – 2.x.2 + 22 = (x – 2)2
– Tại x = -1 : A = ((-1) – 2)2=(-3)2= 9
⇒ Kết luận: Vậy tại x = -1 thì A = 9
Dạng 2 : Chứng minh biểu thức A không phụ thuộc vào biến
Ví dụ: Chứng minh biểu thức sau không phụ thuộc vào x: A = (x – 1)2 + (x + 1)(3 – x)
* Lời giải.
– Ta có: A =(x – 1)2 + (x + 1)(3 – x) = x2 – 2x + 1 – x2 + 3x + 3 – x = 4 : hằng số không phụ thuộc vào biến x.
Dạng 3 : Tìm giá trị nhỏ nhất của biểu thức
Ví dụ: Tính giá trị nhỏ nhất của biểu thức: A = x2 – 2x + 5
* Lời giải:
– Ta có : A = x2 – 2x + 5 = (x2 – 2x + 1) + 4 = (x – 1)2 + 4
– Vì (x – 1)2 ≥ 0 với mọi x.
⇒ (x – 1)2 + 4 ≥ 4 hay A ≥ 4
– Vậy giá trị nhỏ nhất của A = 4, Dấu “=” xảy ra khi : x – 1 = 0 hay x = 1
⇒ Kết luận GTNN của A là: Amin = 4 ⇔ x = 1
Dạng 4 : Tìm giá trị lớn nhất của biểu thức
Ví dụ: Tính giá trị lớn nhất của biểu thức: A = 4x – x2
* Lời giải:
– Ta có : A = 4x – x2 = 4 – 4 + 4x – x2 = 4 – (4 – 4x + x2) = 4 – (x2 – 4x + 4) = 4 – (x – 2)2
– Vì (x – 2)2 ≥ 0 với mọi x ⇔ -(x – 2)2 ≤ 0 với mọi x
⇔ 4 – (x – 2)2 ≤ 4 [cộng 2 vế với 4]⇔ A ≤ 4 Dấu “=” xảy ra khi : x – 2 = 0 hay x = 2
⇒ Kết luận GTLN của A là: Amax = 4 ⇔ x = 2.
Dạng 5 : Chứng minh đẳng thức bằng nhau
Ví dụ: Chứng minh đẳng thức sau đúng: (a + b)3 – (a – b)3 = 2b(3a2 + b2)
* Lời giải:
– Đối với dạng toán này chúng ta biến đổi VT = VP hoặc VT = A và VP = A
– Ta có: VT = (a + b)3 – (a – b)3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3)
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3
= 6a2b + 2b3
= 2b(3a2 + b2) = VP (đpcm).
⇒ Kết luận, vậy : (a + b)3 – (a – b)3 = 2b(3a2 + b2)
• Dạng 6 : Chứng minh bất đẳng thức
– Biến đổi bất đẳng thức về dạng biểu thức A ≥ 0 hoặc A ≤ 0. Sau đó dùng các phép biến đổi đưa A về 1 trong 7 hằng đẳng thức.
Ví dụ: Chứng minh biểu thức B nhận giá trị âm với mọi giá trị của biến x, biết: B = (2-x)(x-4)-2
* Lời giải:
– Ta có: B = (2-x)(x-4) – 1 = 2x – 8 – x2 + 4x – 2 = -x2 + 6x – 9 – 1 = -(x2 – 6x + 9) – 1 = -(x-3)2 – 1
– Vì (x-3)2 ≥ 0 ⇔ -(x-3)2 ≤ 0 ⇒ -(x-3)2 – 1 ≤ -1 < 0 với mọi x,
Dạng 7: Phân tích đa thức thành nhân tử
Ví dụ 1:Phân tích đa thức sau thành nhân tử: A = x2 – 4x + 4 – y2
* Lời giải:
– Ta có : A = x2 – 4x + 4 – y2 [để ý x2 – 4x + 4 có dạng hằng đẳng thức]= (x2 – 4x + 4) – y2 [nhóm hạng tử]= (x – 2)2 – y2 [xuất hiện đẳng thức số A2 – B2]= (x – 2 – y )( x – 2 + y)
⇒ A = (x – 2 – y )( x – 2 + y)
Ví dụ 2: phân tính A thành nhân tử biết: A = x3 – 4x2 + 4x
= x(x2 – 4x + 4)
= x(x2 – 2.2x + 22)
= x(x – 2)2
Ví dụ 3: Phân tích B thành nhân tử biết: B = x 2 – 2xy – x + 2y
= (x 2– x) + (2y – 2xy)
= x(x – 1) – 2y(x – 1)
= (x – 1)(x – 2y)
Ví dụ 4: Phân tích C thành nhân tử biết: C = x2 – 5x + 6
= x2 – 2x – 3x + 6
= x(x – 2) – 3(x – 2)
= (x – 2)(x – 3)
• Dạng 8: Tìm giá trị của x
Ví dụ:Tìm giá trị củ x biết: x2( x – 3) – 4x + 12 = 0
* Lời giải.
x2 (x – 3) – 4x + 12 = 0
⇔ x2 (x – 3) – 4(x – 3) = 0
⇔ (x – 3) (x2 – 4) = 0
⇔ (x – 3)(x – 2)(x + 2) = 0
⇔ (x – 3) = 0 hoặc (x – 2) = 0 hoặc (x + 2) = 0
⇔ x = 3 hoặc x = 2 hoặc x = –2
⇒ Kết luận, vậy nghiệm : x = 3; x = 2; x = –2
Video học 7 hằng đẳng thức đáng nhớ
Kết
7 hằng đẳng thức đáng nhớ là những đẳng thức cơ bản nhất mà mỗi người học toán cần phải nắm vững. Những đẳng thức này được sử dụng thường xuyên trong các bài toán liên quan đến giải phương trình, nhân chia các đa thức, biến đổi biểu thức tại cấp học trung học cơ sở và trung học phổ thông. cmm.edu.vn khuyên bạn nên học thuộc bảy hằng đẳng thức đáng nhớ giúp giải nhanh những bài toán phân tích đa thức thành nhân tử.
Trích nguồn: Cao đẳng Tài nguyên và Môi trường miền Trung
Danh mục: Học thuật









